Ce mois nous continuous avec notre série sur la nature des astéroïdes. En novembre 2019 nous avons considéré comment les orbites des astéroïdes peuvent être changées par l'influence gravitationnelle des planètes majeures.
This month, we turn our attention to the subtle, and more difficult to model and assess, non-gravitational forces which can affect asteroid orbits. Changes to asteroid orbits are very much of interest to humankind as they are critical in the evolution of a benign asteroid into an Earth impacting one.
Ce mois nous considérons les forces non-gravitationnelles qui sont plus difficilement modélisables et qui peuvent avoir un effet sur les orbites des astéroïdes. Des changements d’orbites des astéroïdes sont très intéressants à l'humanité car ils sont cruciales à l'évolution de’un astéroïde inoffensif en un un astéroïde dangereux.
The description we provide here will avoid any maths, an introduction of which is provided in our book on the Asteroids.
Whilst gravitational forces are the dominant forces affecting the orbit of asteroids, there are other, more subtle effects which are also important for accurate orbit determination. This of course is critical for precise computations relating to space missions and PHAs (Potentially Hazardous Asteroids) risk assessments.
Although circa 10 orders of magnitude weaker than solar gravitational forces, the ‘radiation-based’ effects we will briefly look at can be important over long periods of time and have importance for gas and dust (as produced by for example collisions). The forces we will describe are:
Radiation pressure.
This pushes particles radially away from the Sun and the scale of objects sensitive to this are in the range 0.1 to 1.0 micrometres (10**-6 metre i.e. tiny!)
Poynting-Robertson drag.
This causes particles, in the range 1 to 10mm to spiral inwards towards the sun; and the
Yarkovsky effect.
This changes an asteroid’s semi-major axis (increase/decrease depending upon objects direction of rotation) and is effective for asteroids in the range 10m to 10km in rough size.
We will also take a brief look at YORP and asymmetric outgassing, both of which also can affect asteroid orbits. The other radiation type force acting on asteroids is the Solar wind. However, this affects gas and ionised dust. We looked at this in our blog of May 2018 so will not talk about this again here.
Radiation pressure.
Whilst radiation pressure had been conjectured since the time of Isaac Newton, it was not until 1899 that the Russian physicist Pyotr Lebedev (b.1866 d.1912) proved it experimentally and provided measurements.
The Sun emits electromagnetic radiation radially and this is dispersed with increasing heliocentric distance. We can model the amount of radiation emitted, the luminosity of the Sun at any radial distance from the Sun by considering and measuring the solar irradiance received at the Earth.
The earliest direct measurement of the solar irradiance was made in 1838 by Claude Pouillet (b.1790 d.1868) but we now have the benefits of satellite measurements. Regular readers of this blog series will recall we looked at the Solar irradiance in January 2017. The irradiance decreases with the square of the distance from the Sun.
It is useful now to think of radiation here as the out-streaming of photons. Whilst photons are fundamental particles with zero rest-mass, they have both energy and momentum. The momentum of a photon is given by its energy divided by the speed of light. The force acting on a particle at distance is the differentiation of the unit (photon) energy, times by the flux. This force is only significant for very small particles, typically of radius 1 to 10 micrometres (µm, 10-6 m) and decreases with the source intensity and the distance (squared) of the particle from the source.
Poynting-Robertson drag
This effect, usually abbreviated to as the PR drag (or effect), was first described in 1902 by the British physicist John Poynting (b.1852 d.1914) using Newtonian mechanics and gravitation. In 1937, it was enhanced by a more precise relativistic model by the American mathematician Howard P. Robertson (b.1903 d.1961).
The PR drag is similar to radiation pressure, but now takes into account the orbital motion of the particle. It is applicable for larger particles than radiation pressure, affecting particles of a few millimetres in size. This drag (i.e. force of motion resistance) arises due to two aspects of the particles’ motion.
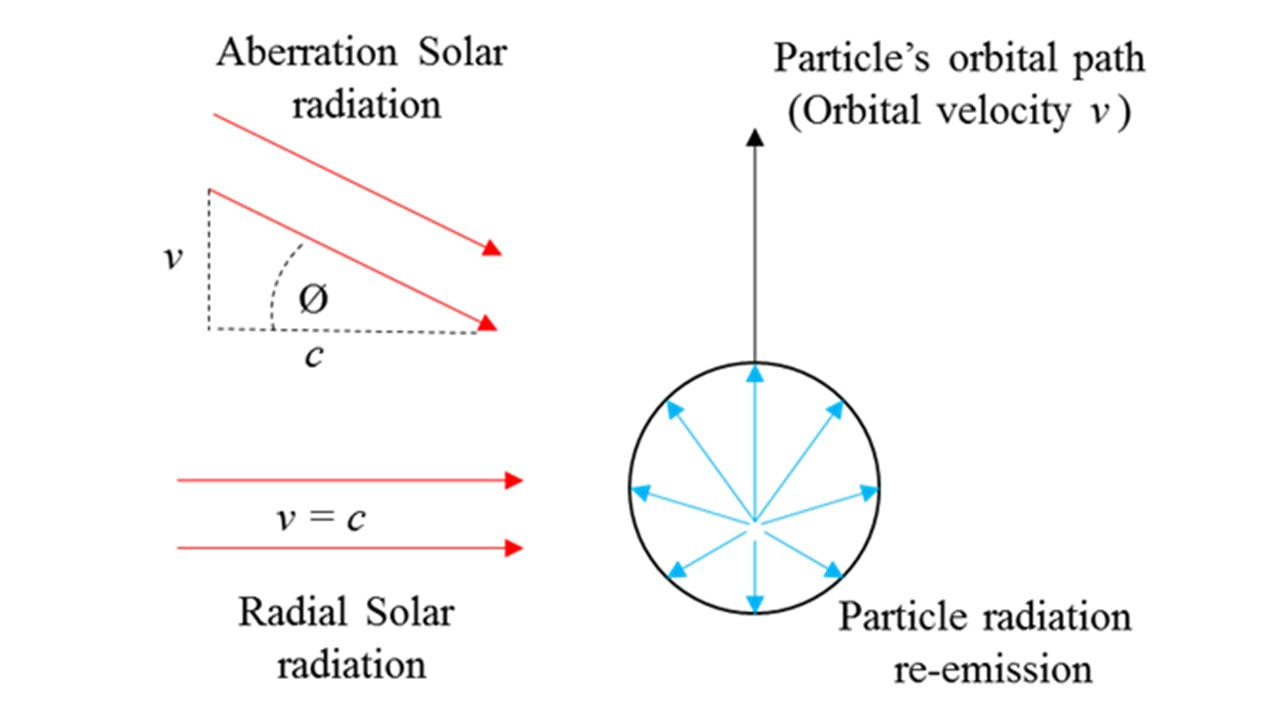
The first aspect is that because the particle is moving, the Sun’s radiation appears to be incident on the particle at a slightly offset angle from the direct radial direction. Hence there is a non-radial component of the radiation vector (equal to sin of resultant incident angle - see diagram below - times the radial force). This means that (even) for particles where the radiation pressure is insignificant compared to the (solar) gravitational force keeping the particle in orbit, there is a radiation pressure (a force) acting in the direction of the particles orbital motion.
The second element is due to the particle’s absorption of the radiation from the Sun and its subsequent re-emittance. Again, because of the movement of the particle, it does not re-emit this radiation isotropically (i.e. consistent in all directions). This is because in the forward direction of travel, the absorption and re-emissions are very slightly higher.
The energy is absorbed and re-emitted across all of the particle, but because of the difference in absorption (and thus re-emittance) between the forward and backwards directions of the particle’s motion, there is a difference in the radiation pressure ‘emitted’ by the particle. This difference in pressure means there is a slightly greater ‘push’ (from Newton’s third law – every force has an equal and opposite reaction) on the front of the particle than on the back.
Yarkovsky and YORP effects
This is similar to the second element of the Poynting Robertson effect and the Yarkovsky effect is due to an asteroid’s absorption of solar radiation, and its subsequent re-emission of thermal (infrared) radiation. The main difference between the two effects is one of operating scale.
First formulated in 1901 by the Belarusian engineer Ivan Yarkovsky (b.1844 d.1902), the effect was seen (and proved) observationally in 2003 by Steven Chesley et al. using radar ranging data collected by the Arecibo radio telescope of the asteroid 6489 Golevka. The effect had been predicted for this asteroid in the year 2000 by David Vokrouhlicky et al. Data sets taken since 1991 showed there had been an increase of 15km in the asteroid’s semi-major axis (so the rate of change was ~ 1km/year).
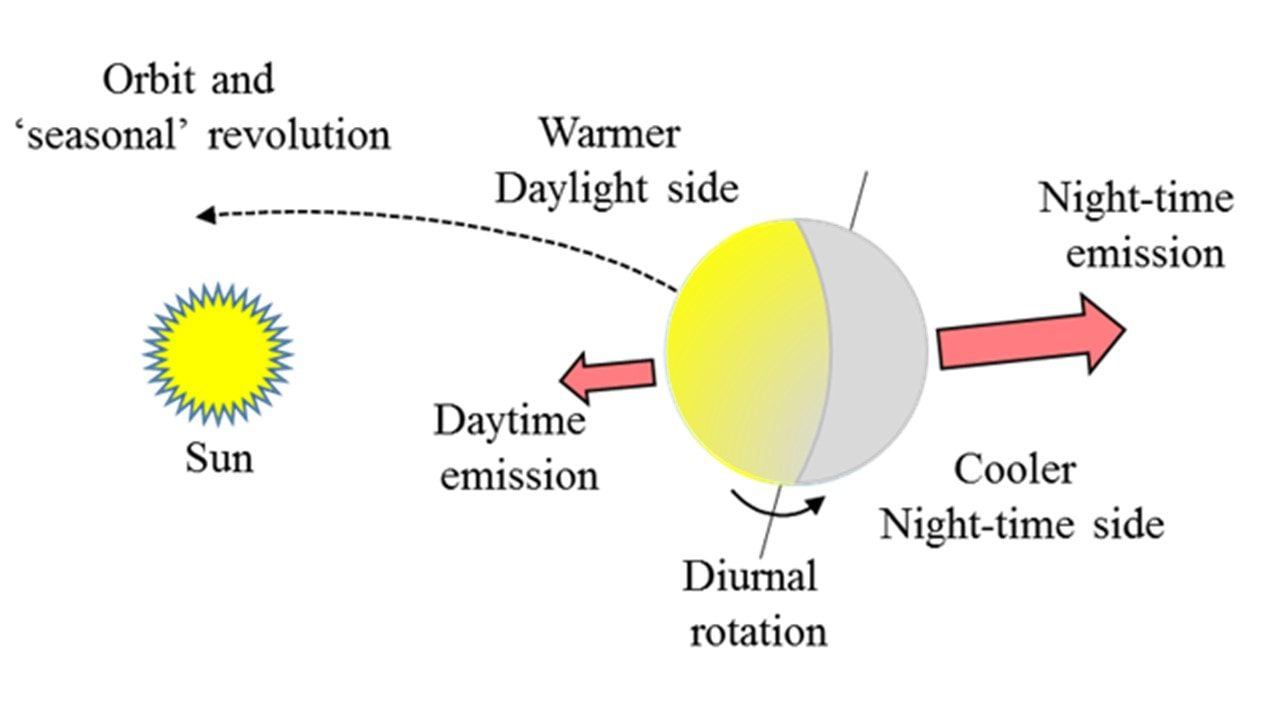
The effect is caused by the anisotropic re-emission of solar radiation. For an area on the surface of the asteroid, the period of maximum absorption by, and least emission of radiation from is when the surface is ‘facing’ the sun, i.e. its ‘daytime’. And conversely, the time of least absorption (zero) and maximum thermal emission is during the surface’s night-time. Looking at the asteroid as a whole, this differential emission on each hemisphere, and particularly at sunrise and sunset times, causes a differential radiation pressure emission. From Newton’s third law (for each force there is an equal and opposite reaction), this leads to a difference in pressure acting upon the asteroid on each side. This difference thus leads to an overall net pressure on the asteroid in the direction of the plane of its orbit
It is most significant for objects of the scale from ~10cm to ~10km, although will have an effect for objects up to ~40km in dimension. The lower end of this scale arises due to the thermal conductivity of the particle being such that there is a very small differential temperature per ‘hemisphere’. The upper range can be assessed by looking at how the asteroid’s mass, and the amount of energy absorbed are dependent upon the size of the asteroid. Radiation is absorbed (and thus the force resulting) in proportion to square of the asteroid’s diameter, whereas the mass of the asteroid is proportional to the cube of its diameter. The acceleration experienced by the asteroid is dependent upon the force and the asteroid’s mass (recall F = ma; hence a = F/m) and so the acceleration experienced by the asteroid due to this force is proportional to 1/diameter. As the asteroid size increases, the acceleration becomes less significant. The effect does not affect the Earth’s orbit!
The consequence of the Yarkovsky effect is that it affects all orbital elements but most noticeably and dominantly, the semi-major axis ; which can either increase or decrease according to the asteroid’s obliquity (by: ). As we have noted above, whilst the orbital changes appear very modest (1km/year for 6489 Golevka) there is a long-term accumulation effect. The Yarkovsky effect is critical for space probe flight dynamics and from a solar system perspective, it important for asteroid orbital migration. To put the consequence in context, the effect is typically of the same order of magnitude as gravitational perturbations on the asteroid due to other asteroids, and very approximately of the order of 10-6 that of perturbations caused by the major planets. However, from a humankind perspective, the effect on PHAs is an important one to be noted. Rather appropriately, 35334 Yarkovsky (1997 FO1) was permanently designated in Yarkovsky’s honour.
YORP effect
The same physical phenomenon that produces the Yarkovsky effect also affects the axial rotation rate, and obliquity, of (non-spherical) objects. The uneven and morphological dependent differential emissions create a thermal torque that restrains, or accelerates, the axial rotation. The same torque leads to a long-term migration of the obliquity towards asymptotic 0 or 180º. This rotational element of the Yarkovsky effect is known at the Yarkovsky-O’Keefe-Radzievskii-Paddack (YORP) effect. It is more subtle than the ‘direct’ Yarkovsky effect, has a more modest, and certainly slower effect.
The YORP effect was first proposed theoretically by the American physicist David Rubincam in the year 2000, and its reality was verified through observation in April 2007. Patrick Taylor et al using radar data from Arecibo and Goldstone radio and radar facilities showed that the spin rate of asteroid 2000 PH5 was increasing at ~2 x 10**-4 degrees per day. This means that the rotation rate of 54509 YORP (as 2000 PH5 became permanently named) which is currently 12.17 minutes per rotation and will halve about every 600,000 years.
It is envisaged that spin rate changes may be one of the sources of production of binary asteroids (where an asteroid’s spin rate is increased beyond the structural coherence of the object, resulting in fragmentation).
Asymmetrical outgassing
Asteroids, almost by definition, do not exhibit coma or diffuse natures. A ‘coma’ in this context is the fuzzy indistinct image caused by solar heating sublimation of the comet’s ices and other volatiles, creating a temporary ‘atmosphere’. Comets undergo ‘outgassing’ and this can and has a significant effect on the comet’s orbit, especially when this is asymmetric (uneven) across the body of the comet.
However, almost entirely, asteroids are not diffuse objects and outgassing is not seen, nor is it a factor involved in their orbital evolution. There are very rare exceptions though and some asteroids have exhibited comet type emissions and a faint coma observed due to outgassing. If an asteroid produces outgassing is it said to be ‘active’.
Next Month
In our next regular blog we will take a look at collisions between asteroids.