Our book on the life and works of François Félix Tisserand is now available as a PDF version. We have also added to the material available for free download in our Educational Resources pages.
Nouvelles
Notre livre sur la vie et les oeuvres de François Félix Tisserand est maintenant disponible en PDF. Vous trouverez aussi plus de ressources à télécharger sur les pages 'Education Resources'.
Stellar fusion and the solar neutrino ‘problem’
As part of our series looking at the nature of the Sun, we considered in January’s blog the solar irradiance. This month we take a look at the energy generation processes which operate within the Sun; nuclear fusion.
The Sun has been generating energy for a very long time. The fossil record indicates that the earliest forms of life arose on Earth sometime between 3.5 and 2.1 billion years ago. So, we can be fairly sure that the Earth’s surface and atmospheric temperature has been at least relatively consistent for the past 3 billion years, and hence by deduction we can assume that the same goes for solar output.
La fusion nucléaire et le problème des neutrinos.
En janvier nous avons considéré l'irradiance solaire; ce mois nous allons étudier de la fusion nucléaire. D'après les traces fossiles les toutes premières formes de vie ont apparu sur la terre entre il y a 3.5 million et 2.5 milliards d'années. On peut être assez certain que la température de la surface et de l'atmosphère de la terre est assez constante depuis 3 milliards d'années etpar conséquent la production solaire.
Life on Earth is unlikely to have been around at the time of the formation of the solar system. An estimate for the age of the solar system can be made by dating meteorites, and thus by implication also an estimate for the age of the Sun. In 1956 Clair Patterson (b.1922 d.1995) dated a residual part of the large meteorite which formed the Barringer crater in Arizona around 50,000 years ago. Using the relative ratios of lead isotopes (207)Pb, (206)Pb and (204)Pb, Patterson determined the meteorite age to be around 4.55 billion years old. This value continues to be the most accepted age of the Earth today and meteorite ageing remains one of the best means of dating the age of the Sun.
It was clear to the scientists of the 18th and 19th centuries that the Sun must have a source of energy to be able to shine. The principal of the conservation of energy had been established and a variety of ideas for the source of the Sun’s power had been considered. The ancients Greeks (e.g. Anaxagoras) considered that the Sun was burning; conversion of gravitational potential energy into thermal (kinetic) energy had been proposed in the mid-1800s by Hermann Von Helmholtz (b.1821 d.1894) and William Thomson (b.1824 d.1907), better known as Lord Kelvin; and in 1904 Ernest Rutherford (b.1871 d.1937) had proposed radioisotope decay as the source. All of these processes had major problems in explaining the rate and longevity of the Sun’s emission and it was not until the 1930s that nuclear fusion processes became known, and evidently were the answer.
Whilst fusion could explain the energy production and the age of the Sun, the ‘theory’ also had issues. The key problem was that the observed rate and energy level of solar originated neutrinos did not meet the theoretical predictions. Solar neutrinos were first detected in 1970 and supported the fusion idea, but by the late 1990s the rate detected was shown to be only one-third of that which should be seen. This conundrum, which became known as the Solar neutrino problem, was finally solved in 1998 when neutrino oscillation, the ability for electron neutrinos to change form, was observed.
Neutrino oscillation had been predicted by Bruno Pontecorvo (b.1913 d.1993) in 1957 and essentially states that neutrinos can exist in 3 different forms; the electron neutrino, the muon neutrino and the tau neutrino. The earlier detectors had only considered the electron variant so were missing around two-thirds in the count. Problem solved? Probably. Neutrino oscillation is also a mechanism whereby the massless neutrino can have a finite mass – although as this is at the forefront of current atomic physics we will not consider this further here.
We will however take a brief look now at the main fusion process which occurs within the Sun, which is the proton-proton chain. This is the process whereby hydrogen fuses to form helium and in doing so, a tiny amount of mass is converted to energy each time a fusion takes place. This tiny amount of mass generates a huge amount of power as described by Einstein’s famous mass energy relationship; the E = mc*c equation. Multiple individual reactions within the high pressure, high temperature of the core generate the totality of the Sun’s power. We will see that there is a natural ‘brake’ on the amount of hydrogen that gets converted, and hence the amount of energy generated, at any one time – which is just as well for the stability of the Sun, and of course for us here on Earth.
Proton-Proton chain
Within the core regions of the Sun, all matter is ionised due to the high pressure, the corresponding high temperature, and hence very high thermal energy of the atoms. At the temperature within the core regions, circa 15-20 million Kelvin, the proton-proton chain (the ‘PP-chain’) is the most dominant (but not the only) process generating power.
The first stage is that 2 hydrogen nuclei (i.e. 2 protons) fuse to form a diproton atom (2 protons)
(1)H + (1)H → (2)He
The diproton, a very unstable isotope of helium, then decays rapidly. Most of the time the diproton decays back to 2 single hydrogen nuclei (protons) but very occasionally, it decays such that one of the protons changes to a neutron by β+ decay ( i.e. p → n + (e+) + ν(e) ) to form a deuterium atom (which is hydrogen with a neutron in the nucleus) along with a positron (e+) and an electron neutrino ν(e) of energy 0.42 MeV. So:
(2)He → (2)H + (e+) + ν(e) [0.42MeV]
The neutrino from this reaction was the ‘source’ of the solar neutrino problem. The ‘overall’ sequence to form deuterium is thus:
(1)H + (1)H → (2)H + (e+) + ν(e) [0.42MeV]
The positron (e+) then reacts extremely quickly with the nearest free electron (e-) in a matter:anti-matter reaction, annihilating both particles but in doing so creating 2 high powered (gamma wavelength) photons, γ, each of around 500 keV and totalling 1.022 MeV.
The deuterium, (2)H, atom then reacts with another proton (ionised hydrogen atom, (1)H ), to form one of the stable forms of helium, (3)He (which has 2 protons and 1 neutron). This reaction produces a high energy (gamma wavelength) photon. The reaction is:
(2)H + (1)H → (3)He + γ [5.49MeV]
The next stage is when 2 helium isotopes, (3)H, atoms formed in this way then fuse to form ‘normal’ helium, (4)He, together with 2 protons (i.e. 2 hydrogen (1)H) atoms. This reaction also produces a high power (gamma wavelength) photon. The reaction is:
(3)He + (3)He → (4)He +(1)H + (1)H + γ [12.86MeV]
Thus, the total energy produced by the fusion process of 4 hydrogen atoms forming 1 helium atom (all ionised) is 2 x (0.42 +5.49+1.022) + 12.86 = 26.72MeV
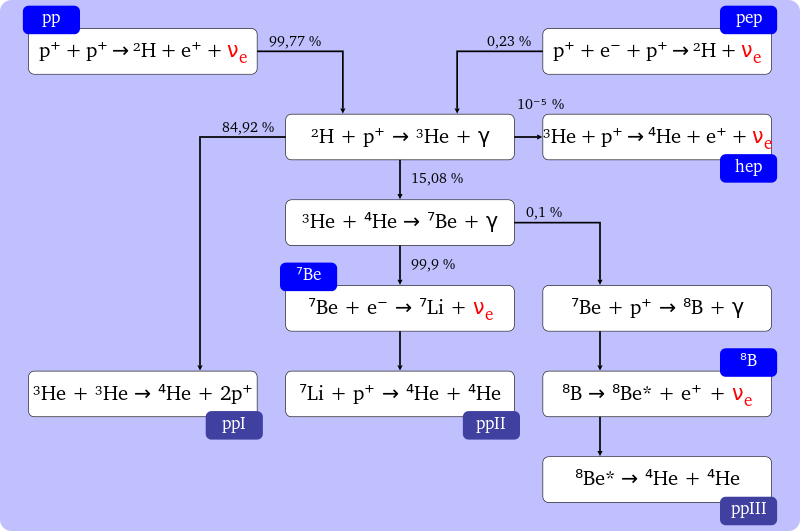
Other proton-proton fusion chain variants
Whilst we have described the highest probability PP-chain (“pp”) above, there are other lower probability reactions that also occur. These are described in the figure below, together with the probabilities of these paths for specific reactions.
https://commons.wikimedia.org/wiki/File%3AProton_proton_cycle.svg
The natural ‘brakes’, most importantly the coulomb barrier, mean that the rate of fusion is governed predominately by the pressure and temperature. The probabilistic and quantum effects of fusion are the reason the Sun does not undergo unrestrained energy creation, i.e. why it doesn’t catastrophically fuse (explode). Such constraints are overwhelmed in supernovae.
We look at topics such as the rate of production, energy and spectrum generated, coulomb barrier and supernovae physics in our book.
In next month’s blog we will look at the energy transfer processes which occur in the Sun. Generating energy is one thing, but how does it dissipate and how does it ‘get-to’ the Earth…?