In our earlier blogs we have seen how an asteroid’s orbit may be slightly changed through either or both gravitational and non-gravitational causes. These changes can, and do, lead to orbits resulting in collisions with other objects. This can include collisions with the major planets; for example, the impact of comet 9/Schumacher-Levy/9 on Jupiter in July 1992; and closer to home, the smaller scale impact on Earth of the Chelyabinsk meteor and meteorite in February 2013, and the Tunguska event in June 1908.
The Earth’s atmosphere shields our surface from many smaller objects. Meteoroids of size below about a few metres, and very dependent on the nature and composition of the meteoroid, are burned to ash/dust in our atmosphere due to frictional heating. However, none of the asteroids have any atmosphere and thus they have no such shield. We can also see this on the atmosphere-less Moon in that any impact will cause a crater (or if the meteoroid is very small, further micro-level erosion of the lunar surface and production of the lunar ‘regolith’).
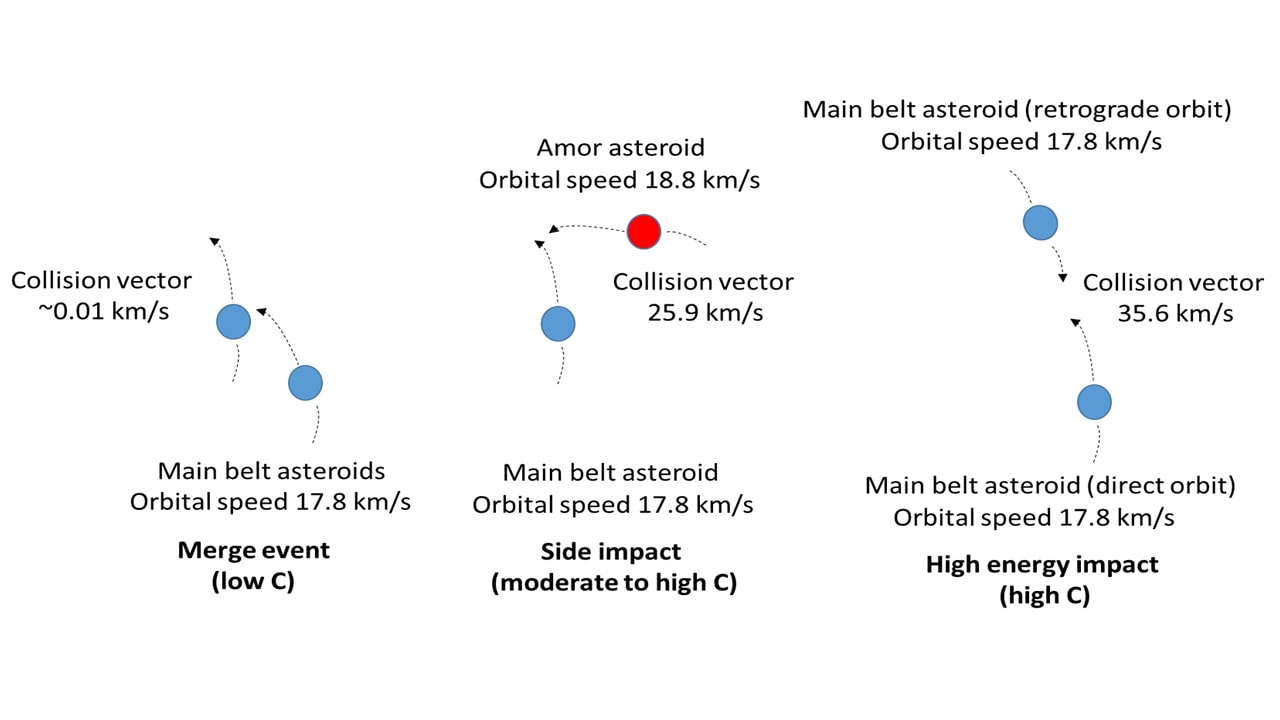
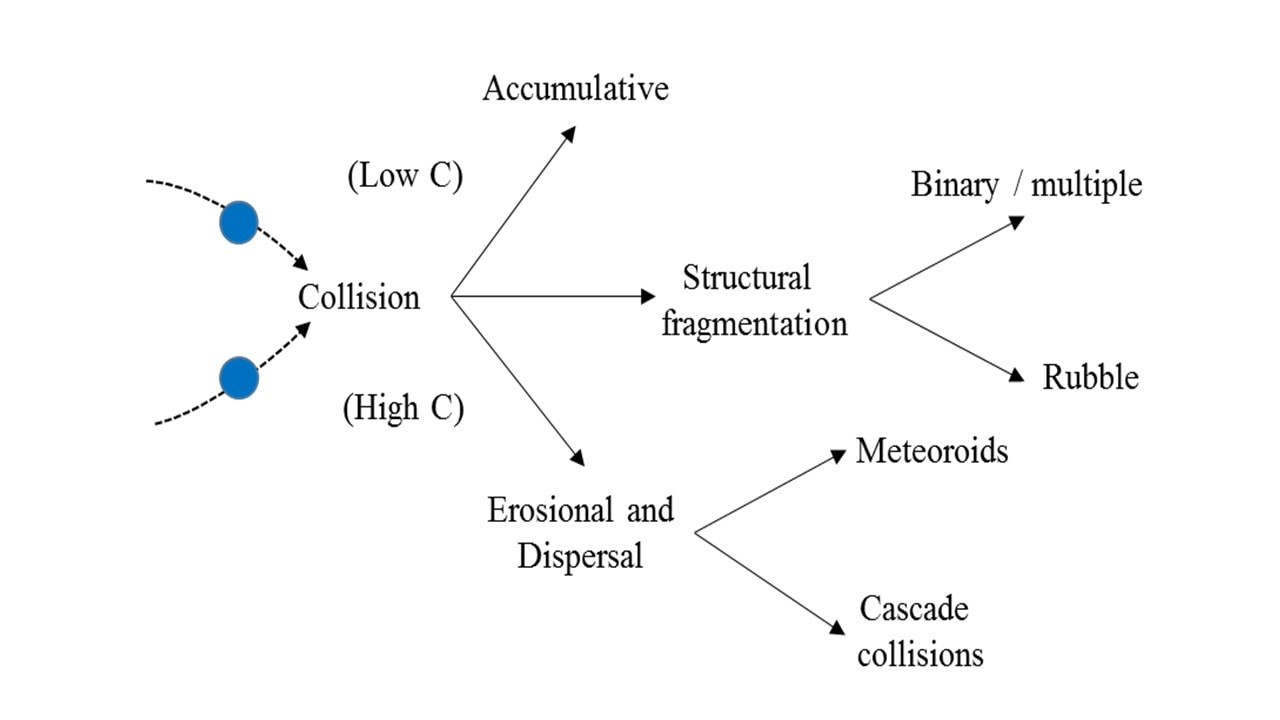
A key factor to determine when two asteroids collide is whether the event is erosional, i.e. the event leads to smaller objects, or accumulative where the result is a larger object alongside impact debris. This depends upon the impact velocity and the size of objects. All types of impact will create dust to a larger or lesser amount. We will consider a smaller object striking a larger object, and look first at the likely velocity of the impact.
We can use energy considerations (and Kepler’s laws) to determine orbital velocity. The orbital velocity of an asteroid in heliocentric orbit with semi-major axis and at a distance from the Sun is given by the formula shown in the equations picture at the foot of this article. Taking the example of a main belt asteroid of semi-major axis 2.8AU in a circular orbit (e = 0), and hence we find its orbital velocity as 17.8km/s.
Now, if we also look at the orbital velocity of say an Amor class asteroid on an elliptical orbit of a = 3.2AU, its speed at 2.8AU will be 18.8 km/second. Looking at the respective orbital directions we can approximate the collision here as a tangential strike and the resultant velocity of impact will be ~25.9 km/second.
We will then compare this to the escape velocity of the larger object. Escape velocity is the speed (radial velocity from the centre of mass of the object) that a particle/object must reach to break free of (attain a hyperbolic orbit with respect to) the larger mass. For a spherical object the escape velocity is again shown in the equations picture below
Looking at an extreme, we can calculate the surface level escape velocity for Ceres, the largest asteroid. This works out to be 0.515 km/second (The Earth’s surface level escape velocity for comparison is 11.2 km/second).
However, for more median sized asteroids, say a typical main belt asteroid with dimension of ~10km and density of 3.0 g/cm**3 (the typical density of stony, chondrite meteorites) the escape velocity is around than 1 m/second (1.4 m/seconds for a homogeneous sphere of this size and density).
Collision dynamics within the main belt will have impact velocities varying between ~0.01 km/second where co-orbiting objects merge by very slow ‘catch-up’, through transverse (sideways) impacts, up to ~40 km/second for ‘head-on’ collisions of asteroids on retrograde and direct orbits respectively.
For high values of C, the event is going to be erosional and likely to lead to fragmentation of one or both objects, and with remnant debris velocities greater than the larger objects escape velocity. For low values of C, the collision will be accumulative (e.g. the smaller particle will impact and remain on the surface of the larger object without producing any high velocity debris). The interesting cases of course are those collisions which lead to fragmentation and structural disruption of the larger object, but with the result being a ‘rubble’ pile where the individual fragments continue in shared orbit and potentially recoalesce (‘re-accretion’).
Next month
We look at the relatively rare and unusual binary asteroids.